构造算法
二维网格放置1x2和2x1方块问题
有一个n行m列的二维网格,你有a个1x2的方块和b个2x1的方块。问是否可以将这些方块不相互覆盖全部放置到网格上。
这是atcoder的一道题目。
这个问题我也没法太清晰地证明,就只是讲讲做法就好了。
首先我们可以很自然地将两个1x2方块或两个2x1方块合并为一个2x2方块,这不是什么难事。
当n和m都是偶数的时候,将2x2的方块往上丢就可以了。
之后考虑当m为奇数的时候,我们可以将最左边那一行先用2x1的方块覆盖。
分两种情况讨论,若n是偶数,那么这意味这最左边那一行可以被完全覆盖(除非$2a<n$)。这种情况下问题就变成了在n行(m-1)列网格放置的问题。
同样如果n是奇数、m是偶数,问题也是同样解决。
下面说一下n是奇数、m是偶数的情况下。这时候不管如何放置都会出现至少一个空位。我们先将最左边那一列用2x1的方块覆盖,最上面的那一列用1x2的方块覆盖,当然我们最后一定会留出至少一个空位,推荐将空位让给第3行第1列。比如考虑5行3列的情况。
^<>
v..
...
^..
v..
我们要的效果就是这样。说一下这样的好处。当剩下的a和b都是奇数的情况下,原先我们会浪费1个2x2的空格。
^<>
v<>
...
^^.
vv.
但是,这里我们可以避免2x2空格的浪费,考虑下面的方法:
^<>
v.^
<>v
^..
v..
因此,当a为4,b为3的时候,正确的做法如下:
^<>
v.^
<>v
^<>
v<>
置换排序
给定一个$0$到$n-1$的置换$p_0,p_1,\ldots,p_{n-1}$,你每次操作可以选择一个下标$i$,并交互$p$序列中第$i$个和第$(i+p_i)\pmod n$个元素。要求用少于$2\times 10^5$次操作,将序列排序。其中$1\leq n\leq 100$。
有一个比较简单的随机做法。我们可以不断随机操作,直到排列中只包含一个大环。假如数据是随机的情况下,排列中仅含一个环的概率为$\frac{1}{n}$。
在只有一个环后,之后对$0$位置做$n-1$次操作就会将序列排序。(此时$p_0$会交换到正确的位置,之后$p_0$会变成环上的下一个元素,且$0$处于环的末尾)。
提供一道题目。
Floyd判环
有一个如下图的图,有十颗棋子一开始处于起点,只能沿着箭头移动。你不知道$t$和$c$,你每回合可以让任意颗棋子向前移动一步,移动后交互器会告诉你目前哪些棋子落在同一个位置。要求你最后将所有棋子都抵达终点(环的入口),使用的总回合数不能超过$3(t+c)$。
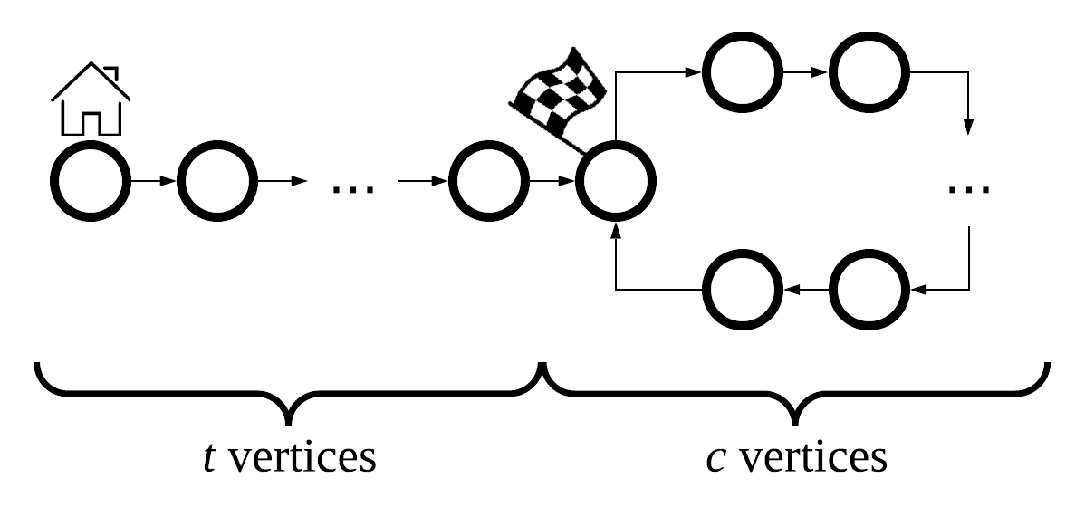
一道题目。
神奇的解法,以前确实做过类似的龟兔赛跑来判环的方法,但是确实从来不知道用三个棋子,3(t+c)步就可以得出t和c的所有信息。
首先,我们可以用棋子0和棋子1做龟兔赛跑,棋子0每次走两步,棋子1每次走一步。直到二者在环上距离入口$x$处相遇。这时候0走的距离为$t+x+kc$,1走的距离为$t+x$(1肯定没有走完整个循环)。而由于0走的距离是1的两倍,因此可以推出:$t+x=0\pmod c$。这意味着当我们将所有棋子每次都向前移动一步,那么至少需要$t$步才能保证所有棋子都走到循环的入口,同时t步也正好能保证所有棋子来到循环的入口。