析合树
本篇文章内的图片全部来自于析合树 OIWIKI。
析合树
考虑这样一个问题,给定一个$1$到$n$的排列$P$,如果$P_l,P_{l+1},\ldots,P_r$排序后是一段连续的数值,或者说$\max_{l\leq i\leq r}P_i-\min_{l\leq i\leq r} P_i=r-l$,那么我们称$(P,[l,r])$是一个连续段。
可以发现连续段拥有如下性质:
- 如果$1\leq a\leq l\leq b\leq r\leq n$,且$(P,[a,b])$和$(P,[l,r])$都是连续段,那么它们的交集$(P,[l,b])$,并集$(P,[a,r])$,差集$(P,[a,l))$和$(P,(b,r])$都是连续段。
可以发现连续段的数目是$O(n^2)$的,这有点太多了。现在我们引入本原段的定义:
- 本原段:一个段是本原段,当且仅当不存在另外一个连续段与其部分相交。
可以发现本原段之间只有包含关系,而不存在相交关系。因此我们可以将所有本原段组织为一颗树。考虑到树的叶子结点是$n$个单一元素的连续段,且每个非叶子顶点下至少拥有两个孩子,因此可以证明本原段的数目是最多有$2n-1$个。
在本原段组成的树中,一个顶点拥有多个孩子。我们可以将孩子按照它们的下标顺序从小到大排序成一个列表,这样的列表我们称为该顶点的儿子序列。之后我们根据孩子序列中每个孩子中的值进行离散化,得到一个新的排列,这样的排列叫做儿子排列。
下面我们引入析点和合点的定义:
- 合点:如果一个顶点的儿子排列是递增或递减的,则这个顶点为合点。
- 析点:一个顶点是析点当且仅当这个顶点不是合点
有了这两个定义,我们就可以将所有本原段划分为两类:析点和合点。
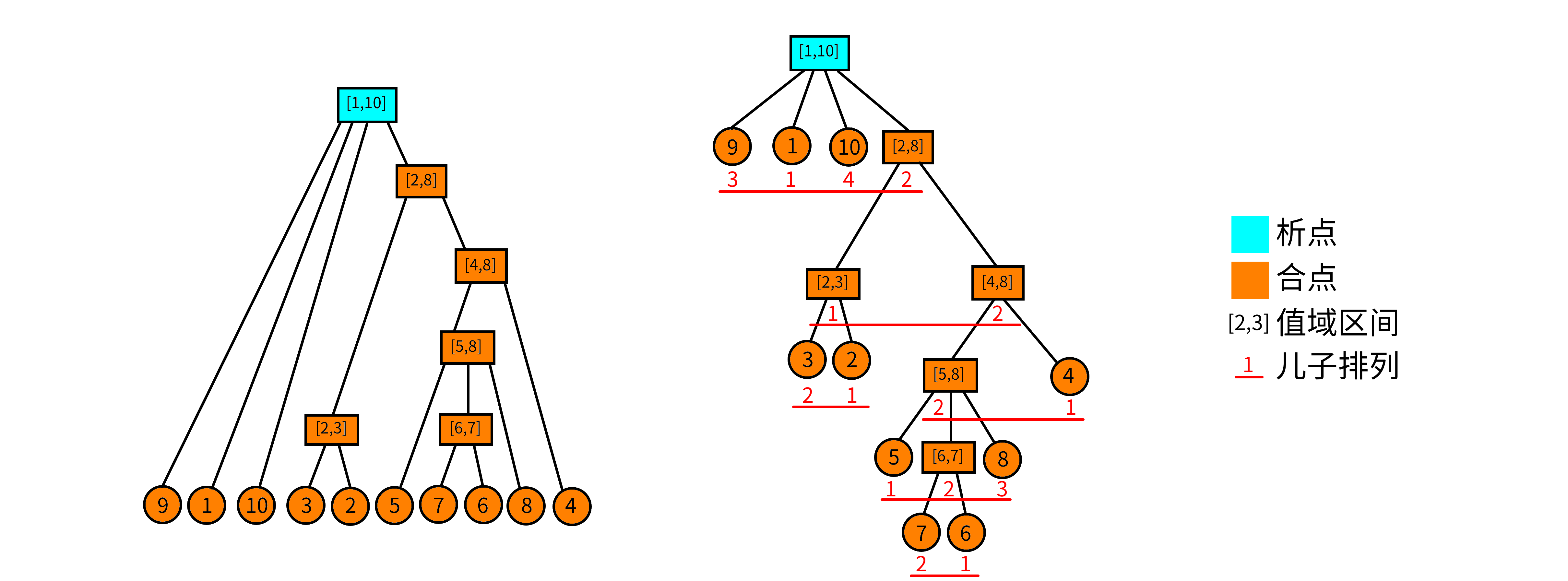
当一个顶点是合点的时候,那么它的儿子序列中任意连续的几个孩子都可以组成一个连续段。而当一个顶点是析点的时候,它的儿子序列中连续的至少两个孩子组成的序列都不是连续段。
根据上面这个性质还可以推出析点至少拥有四个孩子。否则第二大的孩子可以和左右结合。
根据析合树的定义,我们可以发现所有连续段要么是一个本原段,这时候对应析合树上的一个顶点,要么不是本原段,这时候它对应某个孩子序列中连续的至少两个孩子组成的序列。
上面这个性质允许我们通过析合树高效处理所有的连续段。
下面讲讲如何建立一颗析合树。
我们可以利用增量的方式来构建一颗析合树。假设我们已经根据前$k$个数值构建了一个析合树森林,我们将森林的根结点按照处理顺序保存在一个栈中。接下来考虑设第$k+1$个数。首先我们可以构建一个值域为$[P_{k+1},P_{k+1}]$的本原段,记这个本原段为$x$,记栈顶部的顶点为$y$,我们需要做下面操作:
- 如果$y$是一个合点且拥有至少两个孩子,且$x$可以作为$y$的新儿子,那么将$x$加入到$y$的儿子序列中,之后$y$出栈并令$x=y$。
- 如果第1步没有成立,则尝试创建一个新合点$z$,它的孩子为$y$和$x$,之后将$y$出栈并令$x=z$。
- 如果前面几步都不成立,创建一个析点$z$,并将$x$和栈顶部尽可能少的顶点作为$z$的孩子并出栈,最后令$x=z$。
- 如果前面几步都不成立,将$x$入栈,并结束流程。

上面的算法瓶颈实际上在第三步,因为很可能第三步没有满足,但是我们被迫需要扫描整个栈。因此如果就使用naive的算法的话,时间复杂度会达到$O(n^2)$。
要优化上面的算法,我们必须减少第3步需要的扫描次数(出栈入栈其总的时间复杂度为$O(n)$可以无视)。
假设给定区间$[a,b]$,记$[l,r]$为包含所有值落在$[\min_{a\leq i\leq b}P_i,\max_{a\leq i\leq b}P_i]$范围内的最小区间。如果$r>b$,则可以发现以$b$作为右端点,以小于等于$a$的数作为区间左端点的区间一定不是一个连续段。因此在第三步的时候,如果我们倒着扫描栈,一旦发现当前合并的区间中,此时算出的$r>k+1$,则可以直接退出。当然这个过程是微不足道的,但是如果我们结合fail链的技术,比如说新插入的顶点$x$的fail链指向第一个遇到的$r>k+1$的顶点。这时候我们可以$y.fail$解读为要合并$y$和前面一个顶点必须先同时合并掉$y.fail$。这样的话扫描的时候就可以沿着fail链来做操作,第三步的总的时间复杂度就优化到$O(n)$了。
然后我们还需要$O(1)$计算区间最小最大值的技术,我们可以通过结合笛卡尔树+Schieber Vishkin算法实现。
上面讨论的这个算法的时间复杂度为$O(n)$。
题目1:给定一个长度为$n$的置换$P$,要求回答其中有多少连续段。这里$1\leq n\leq 10^6$。
求出析合树后,可以发现每个本原段(顶点)都对结果贡献1,而每个拥有$k$个孩子的合点,对结果贡献${k\choose 2}-1$。
时间复杂度为$O(n)$
题目2:给定一个长度为$n$的置换$P$,之后回答$m$个请求。每个请求给定$l,r$,要求找出最小的连续段$(P,[a,b])$,满足$a\leq l\leq r\leq b$,结果保证唯一。这里$1\leq n\leq 10^6$
首先求出析合树,可以发现$[l,l]$和$[r,r]$对应的是析合树上的叶子结点。找到二者的LCA,如果LCA是析点,则结果就是LCA代表的本原段,否则我们可以取二者在LCA孩子列表中二者之间的所有孩子组成的连续段。
这里我们可以在树上做倍增,时间复杂度为$O(n\log_2n)$。
提供一道题目。
题目3:给定一个长度为$n$的置换$P$,之后回答$m$个请求。每个请求给定$l,r$,要求计算$P_l,P_{l+1},\ldots,P_r$的子序列中有多少是连续段。这里$1\leq n,m\leq 10^6$
提供一道题目。
首先我们可以在$P$上建立一颗析合树。
之后对于每个请求,我们实际上可以遍历一遍析合树就可以找出所有落在区间的连续段的数目,因此对于每个请求的时间复杂度为$O(n)$。
我们考虑从$L=[P_{l-1},P_{l-1}]$和$R=[P_{r+1},P_{r+1}]$这两个叶子之间的路径。可以发现路径上的所有顶点都不处于区间中。路径将树划分为两部分,路径内部的顶点都是属于区间的,外部的顶点都是属于区间外的。
我们可以为每个顶点$u$赋予一个$c$属性,即$u.c$表示的是以$u$为根的子树存在多少连续段。记$u.a$表示以$u$所在儿子列表中以$u$开始的后缀中顶点集合所对应的子树所存在的连续段数目,同时记$u.b$表示以$u$所在儿子列表中以$u$开始的后缀中顶点集合所对应的子树所存在的连续段数目。
之后我们记$A$为$L$和$R$的LCA,记$LA$为$A$的孩子中包含$L$的顶点,同理记$RA$为$A$的孩子中包含$R$的顶点。于是我们可以发现从$L$到$LA$的路径上我们取顶点的$a$属性,从$R$到$RA$的路径上我们取顶点的$b$属性,而对于$LA$和$RA$我们需要特殊判断。
要处理路径,我们可以使用LCT、树链剖分。但是由于不存在修改操作,我们可以使用更加简单的树上前缀和的技术,利用直链剖分快速找到$LA$和$RA$。
这样预处理的时间复杂度为$O(n\log_2n)$。之后每个请求都可以$O(1)$回答。