最大流算法
- 上下界最大最小流
- 最小割
- 最大权闭合图
- 独占路问题
- 最大密度图
- 最小费用最大流
- 最小割树(Gomory-Hu Tree)
- Dinic解决单位图最大流
- 最小费用修复网络问题
- 费用流解决二分图标签问题
- 参考资料
上下界最大最小流
无源汇有上下界可行流
题目:给定$n$个点和$m$条边组成的图$G$,每条边都有一个流量上限和下限,求一种流量方案,使得每个顶点流量平衡且每条边的流量都合法。
首先我们让图上跑着一个流$F$,每条边上的流量都是它的下限。这个流如果是不可行的,那么只有一个可能,一些顶点的流量不守恒。我们可以建立另外一张图$G'$,每条边的容量为上限减去下限。由于一些顶点的流量不守恒,我们可以选择释放或追加一些流量来帮助其平衡。做法就是加入一个新的源点和汇点,之后对于每一条边$(u,v)$,我们建立一条从源点到$v$的边,同时建立一条从$u$到汇点的边,容量均为$(u,v)$的下限。
在图$G'$上跑出最大流$F'$后,我们检查每个与源点和汇点相连的边是否被跑满了流,如果不,就无解。因为如果存在可行流,我们将所有边的流量减去下限,这样原图的部分顶点流量就会不守恒,不守恒的部分会借由与源点相连的边或与汇点相连的边流入或流出,这样就能得到跑满的最大流了。
在图$G'$上跑出最大流$F'$后,我们发现$F'+F$是一个可行流,只要删除源点和汇点即可。
LOJ上的模板题
有源汇有上下界最大流
题目:给定$n$个点和$m$条边,其中顶点$1$是源点,顶点$n$是汇点。每条边都有一个流量上限和下限,求一种流量最大的方案,使得每个顶点流量平衡且每条边的流量都合法。
首先我们跑出一个可行流。但是这里与无源汇有上下界可行流优点不同,就是顶点$1$和$n$允许流量不守恒,准确的说$1$允许入流减出流为负数,而$n$允许入流减出流为正数。这里我们可以从$n$到$1$加一条辅助边,边的容量为无穷。这样跑出了可行流后,删除辅助边得到的还是可行流。
接下来我们考虑如何在可行流的基础上找到最大流,如果我们直接在可行流上跑,就会导致一些边的流量低于下限。简单的方式就是我们在图$G'$的残存网络上跑从顶点$1$到顶点$n$的最大流,尽管图上原先加入的源点和汇点会的流量不守恒,但是与它们相连的边的流量是不会改变的,因此可以直接忽略原先的源点和汇点。。
LOJ上的模板题
有源汇有上下界最小流
题目:给定$n$个点和$m$条边,其中顶点$1$是源点,顶点$n$是汇点。每条边都有一个流量上限和下限,求一种流量最小的方案,使得每个顶点流量平衡且每条边的流量都合法。
类似于有源汇有上下界最大流,我们先跑出一个可行流,不同点是最后是从$n$向顶点$1$跑最大流,即我们要回退尽可能的流。
LOJ上的模板题
最小费用可行流
给每条边赋予一个费用以及流量的上下界,要求找到最小费用可行流。具体的做法是先构建一个辅助网络(增加超级源点汇点以及一系列边),之后在上面跑最小费用最大流即可。或者可以先跑出任意一个可行流,之后通过消圈算法来将流优化为最小费用可行流。
最小割
从网络流中删除总容量最少的边,使得s所在连通块与t所在连通块不连通,被删除的边集称为最小割。
对于一般图的最小割是指删除权重和最小最的无向边,使得S与T不相连。这里建模网络的时候权重为$w$的无向边应该表示为两条反向的容量为$w$的有向边(或一个容量为$2w$而流量为$w$的边)。
最小割最大流定理:最小割的总容量与网络中最大流相等。
我们要求$s$与$t$最小割,可以通过最大流算法跑出最大流,之后将与$s$连通的顶点集合记作$S$,将与$t$连通的顶点集合记作$T$,这时候$S\cap T=\emptyset$,而所有从$S$到$T$的边都是被割去的边。
题目1:给定一个包含$n$个顶点$m$条边的无向图,每条边都有删除成本(正数),希望删除一组总成本最小的边,使得顶点$1$和$n$不连通。
这是一个典型的最小割问题,对于每条边$(u,v)$,记其费用为$c$,我们在网络中加入一条容量为$c$的双向边(注意也需要是双向的)。之后找到最小割即可。
题目2:给定一个包含$n$个顶点$m$条边的无向图。每个顶点都有删除成本,希望删除一组总成本最小的边,使得顶点$1$和$n$不连通。保证顶点$1$和$n$之间没有边。
我们把每个顶点$i$拆分成$X_i$和$Y_i$两个顶点,两个顶点之间加入一条容量为删除成本的双向边。这样删点可以转换为删除边。之后对于每条图中的双向边$(u,v)$,其中$u,v\neq 1,n$,我们对应加入一条$Y_u$到$X_v$以及从$Y_v$到$X_u$的容量为无穷的单向边。对于边$(1,u)$,我们在源点到$X_u$之间加入一条容量为无穷的单向边,而对于边$(v,n)$,我们在$Y_v$向汇点连一条容量为无穷的单向边。
题目3:给定一个流网络,其中除了源点$s$和汇点$t$外还有$n$个顶点,源点到第$i$个顶点有一条容量为$a_i$的边,而第$i$个顶点到汇点有一条容量为$b_i$的边,且对于任意$i<j$,存在一条从$i$到$j$的容量为$c$的边。要求计算最大流。
提供一道题目。
这个问题用最大流求,时间复杂度至少为$O(n^3)$。但是如果用最小割求,则可以优化到$O(n^2)$。
具体做法是记$dp(i,j)$表示前$i$个顶点,割后属于$S$的顶点有$j$个的最小割边费用。可以发现这个DP的转移是$O(1)$的,因此时间复杂度为$O(n^2)$。
平面图最小割
给定$n\cdot m$矩阵,左上角是起点,右下角是终点。有些网格是不可通行的。且两个相邻的顶点之间存在一条边,边权给定。现在求该图的一个最小割。其中$n,m\leq 1000$。
直接上最小割会TLE,因为图太大了。要解决这个问题,我们需要知道如果将平面图转换成对偶图,转换成对偶图后,原图的每个割都对应对偶图中从起点到终点的一条路径,而最小割则对应最短路。因此问题可以通过dijkstra算法解决,时间复杂度为$O(nm\log_2nm)$。
提供一道BZOJ题目。
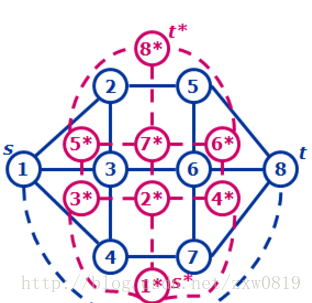
这里推荐一篇博客,里面讲解了怎么将平面图转换为对偶图,顺便借一张图。
最多割集划分
给定一个包含$n$个顶点,$m$条边的无向图,给定起点$s$和终点$t$,要求找到最多的不相交边集,使得任意一个边集的删除都会导致$s$和$t$的不连通(即边集是$s$到$t$的一个割集)。
讲一下我的思维轨迹吧,这道题还是比较取巧的。
首先这个题目问的是存在多少割,注意到如果图是平面图,那么我们将其转成对偶图,问题就变成了存在多少从起点到终点的不相交的路径,这个是独占路问题,可以用最大流求解。
到这里一切都很完美,直到我发现图不一定是平面图。
接下来就可以尝试非常直接的想法,从起点跑最短路,之后将图分成$d(t)$层,我们之后可以给出$d(t)$个不相交边集,其中第$i$个边集由距离为$d(i)$与$d(i+1)$的顶点之间的边构成。
可以发现这个想法中,得到的结果一定是不相交的,同时每个集合也都是原图的一个割集。现在只需要证明不存在数量更大的不相交割集。
这个一开始我用的归纳法,发现不好证明。但是紧接着发现一个非常简单的证明方式:任意考虑从$s$到$t$的一条最短路,其长度为$d(t)$。很显然每个割集都至少会包含这条最短路上的至少一个顶点(否则就不是割集了),而这些割集又不相交,因此可以直接推出不相交割集的数目上限为$d(t)$个。
时间复杂度为$O(n+m)$。
提供一道题目。
最大权闭合图
对于一个有向图$G=(V,E)$,我们称$V$的一个子集$U$为闭合图,如果对于所有边$(u,v)\in E$,有$u\in U\Rightarrow v\in U$。
如果每个顶点都有对应的权值,称总权最大的闭合图为最大权闭合图。
我们可以建立一个对应的图$G'=(V',E')$来计算最大权闭合图。我们通过向V中加入两个新结点$s$,$t$得到$V'$,即$V'=V+{s,t}$。而对于$E$中的每一条边,我们在$G'$中建立对应的一条边,但是容量设为无穷。对于每一个结点$u$,如果$w(u)$的权大于$0$,我们则建立一条边$(s,u)$,容量为$w(u)$。而如果$w(u)$为负数,我们就建立一条边$(u,t)$,容量为$-w(u)$。如果$w(u)$为$0$,那就不用管。
考虑$G'$中的一个最小割,由于流量最多为所有结点权值之和,因此最小割中的边容量均不可能超过该上界,即原图中的有向边(容量为无穷)不会出现在最小割中。
简单割是指这样的一个割,其中每条边至少有一个端点为$s$或$t$。而很显然图$G'$只有简单割。
最小割将$V'$划分为两个连通的集合$S$与$T$。而$X=S\cap V$一定是一个闭合图,否则就存在这样一条边$(u,v)\in E$,$u\in X$且$v\in V-X$,但是这也说明$X$与$v$不连通,即边$(u,v)$属于最小割,而这与最小割是简单割相悖。
对于任意闭合图$X$,我们可以选择从$G'$中删除所有从$X$到$t$的边,以及从$s$到$V-X$中的边,这些边组成的就是最小割,而剩下的$S=X+s$。
我们记$A=S-s$,$B=T-t$,记$A^+$表示$A$中所有权重大于等于$0$的结点集合,而$A^-$表示$A$中所有权重小于$0$的结点集合,对于$B$同样。
由于简单割覆盖了所有$S$到$t$的边,以及$s$到$T$的边,因此简单割应该满足$cut(G')=B^++(-A^-)$,这里表示的集合中所有结点的权值之和。
而图A的权值之和应该为满足下面性质:
\[A=A^++A^-=A^++B^+-(B^+-A^-)=V^+-cut(G')\]这里$A^+$表示的是集合$A^+$的总权值,其它类似。当$A$的总权值最大时,显然$cut(G')$最小,因此我们只需要计算出图$G'$的最小割之后代入上面公式即可得到闭图的最大权,而闭图此时为$S-s$。
提供一道Atcoder的题目。
题目1:给定一个依赖图(无环),但是所有依赖关系都是带权的,即$(a,b,c)$表示$a$依赖$b$,但是如果不执行$b$,也可以通过负担一个指定的惩罚$c$来继续执行$a$。现在求最大闭合子图。
在我们将依赖图转换为网络流的时候,针对依赖$(a,b,c)$,我们从$a$向$b$连一条容量为$c$的边而非容量无穷即可。
之后直接通过最大流找最大闭合子图。
提供一道题目。
独占路问题
问题1:给定一副$n$个顶点$m$条边的无向图。现在希望找到$k$条从顶点$1$到顶点$n$的路径,且所有路径都没有公共边。
我们可以建立一个网络流,每条边的容量均为1,之后找到任意一个流量为$k$的流即可。那么如果从流中提取出$k$条路径呢,非常简单我们直接从顶点$1$开始DFS,直到抵达顶点$n$为止。由于除了源点和汇点外,其余所有顶点都是流量平衡的,即入流等于出流,因此我们一定能找到这样的$k$条路径。每次找到路径后,删除路径中出现的边,总共跑$k$次DFS即可。
时间复杂度为$O(\min(n^2m,km))$。
问题2:给定一副$n$个顶点$m$条边的无向图,每条边都有一个长度。现在希望找到$k$条从顶点$1$到顶点$n$的最短路径(每条路径都是最短路),且所有最短路径都没有公共边。
在问题1的基础上,我们将网络流替换成费用流,每条边的费用为长度,容量为1。假设最短路为$L$,那么我们只要要求流量为$k$的最小费用流费用正好为$kL$即可。首先由于沿最小费用路径增广,每次的增广的费用都是非严格递增的,而第一次增广的费用为$L$,因此增广$k$次的费用至少为$kL$。同时如果存在满足条件的$k$条路径,一定可以搞出这样的流。现在来考虑第二个问题,我们DFS出来的路径一定是最短路,这是必然的,假如我们DFS出长度超过$L$的路径,那么剩下的$k-1$条增广路径的总费用小于$(k-1)L$,这与$k-1$的最小费用流的费用至少为$(k-1)L$相悖。
时间复杂度为$O(knm)$。
最大密度图
假设有图$G=(V,E)$,要求找其中一个子图$G'=(V',E')$,使得边数与顶点数的比值尽可能大:
\[\max \phantom{1}\frac{|E'|}{|V'|}\]符合上述条件的图称为最大密度图。
由于是分数最大化,且分母始终大于$0$,很容易想到分数规划。分数规划通过不断解决下面过程来二分搜索最终的结果:
\[h(c)=max\{|E'|-c|V'|\Big|G'=(V',E')\subseteq G\}\]要解决上面的问题,我们可以创建一个新图,为G中每个结点和边都在新图中建立一个对应结点,边对应的结点的权值为$1$,而结点对应的结点的权值为$-c$。由于选择某条边加入$G'$的前提是边的两个端点都已经加入了$G'$,因此我们需要在新图中建立对应的依赖关系,从边对应的结点向其端点添加一条单向边。到此,求解$h(c)$的问题已经转换成了最大权闭合图问题。
由于对于任意两个密度不同的子图$A=(V_A,E_A)$和$B=(V_B,E_B)$,不妨设图$A$的密度大于图$B$。那么有
\[\frac{|E_A|}{|V_A|}-\frac{|E_B|}{|V_B|}=\frac{|E_A||V_B|-|E_B||V_A|}{|V_A||V_B|}\geq \frac{1}{|V_A||V_B|}\geq \frac{1}{|V|^2}\]因此我们二分的精度可以设为$\frac{1}{|V|^2}$,二分的上界为$|E|$,而二分的下界为$0$,总共二分次数为:
\[\log_2{\frac{|E|-0}{\frac{1}{|V|^2}}}=O(\log_2|V|)\]最小费用最大流
每次沿着费用最小的路增广得到的最大流就是最小费用最大流。随着不断增广,最小费用路径的费用和会越来越大。
目前所有通过最小费用路径增广的算法都不具有多项式时间复杂度,其时间复杂度与最大的流量相关联。Codeforces上有相关的讨论。
Dijkstra算法优化最小费用最大流
通过最小费用路径增广最小费用最大流算法,一般采用的都是Spfa搜最小费用路径,这样的话时间复杂度应该为$O(VEf)$,其中$f$是最大流。
但是事实上我们可以利用与Johnson算法类似的思想,将所有边权全部修正为非负。
具体做法是这样的,我们先对原始网络跑出没个顶点从源点出发的最短距离(第一次利用Spfa算法跑),之后修正边$(u,v)$的权重为$W(u,v)+D(u)-D(v)$,由最短路的性质知道$D(u)+W(u,v)\geq D(v)$,很显然此时的图中不存在负权边。
现在考虑增广了流后残存网络的变化:新的边加入以及旧的边被删除。
考虑新的边$(v,u)$被加入,这意味着$(u,v)$在该次增广时处于最短路径上,那么就一定有$D(v)=D(u)+W(u,v)$,而$(v,u)$的权重将被修正为$W(v,u)+D(v)-D(u)=0$,即没有负权边加入。
旧的边被删除并不会破坏图中无负权边的性质,可以不用考虑。
因此总的时间复杂度为$O(f(V+E)\log_2V)$,不管咋说,都要比Spfa的版本的好。
容量缩放+消圈算法
我们知道通过最小费用路增广的最小费用流算法是可以被卡到指数级的,这时候即使只有40个顶点,也是在几秒有限时间内无法算出结果的。
下面讲一个可以在$O(VE^2\log_2U)$时间复杂度内结束的伪多项式时间复杂度的算法。由于实际问题中精度一般有限,因此我们可以认为$\log_2U\leq 60$。当然这个算法只适合用于整数容量(如果是浮点数,那么必须牺牲一些精确度,将其转换为整数,比如乘上一个较大的数,最后再除去)。
下面讲一下具体做法。
首先我们从汇点向源点连一条费用为负无穷,容量为无穷的边。于是这样取到最小费用流的同时也会得到最大流(如果不要求最大流,可以将这条边的费用设为$0$)。
首先我们将所有边的流量设置为0,并将流量上限设置为0。之后我们记所有边最大的容量为$C$,我们枚举一个变量$x$,初始值为$\lfloor \log_2C \rfloor$。
当我们枚举某个$x$的时候,且网络没有负权环。那么我们将所有边的上限翻倍同时将流量翻倍,可以发现网络中依旧不存在负权环。如果某条边的容量的二进制的第$x$位为$1$,那么我们将这条边上限提高$1$。这时候可能会引入负权环,此时负权环一定包含这条边。设这条边为$(u,v)$,在扩容前,我们可以通过Spfa算法找到从$v$到$u$的最短路,长度记做$d(u)$。如果$d(u)+cost(u,v)<0$,这表示是一个负环,我们在负环上跑一单位的流。跑完后,我们可以证明图中不再存在负权环。
因此我们发现每条边最多扩容$\log_2U$次,每次扩容消环的时间复杂度为$O(VE)$,因此总的时间复杂度为$O(VE^2\log_2U)$。
最小割树(Gomory-Hu Tree)
强烈推荐一发博客,我也是看这篇博客学会的。
下面讲一下自己的理解。
假设给定一个拥有$n$个顶点$m$条边的连通无向图$G=(V,E)$,每条边有一个边权,而图上的从$s$到$t$的割就是$E$的一个子集$E'$,使得从$G$中删除所有$E'$的边后,那么$s$与$t$就不再连通。而所有割中割去的边的总权值最小的称为最小割。网络流中证明了最小割恒等于最大流。这里我们记$F(s,t)$表示$(s,t)$的最小割的权值之和。
而$G$的最小割树是一颗拥有$n$个顶点的树$T$,对于$T$的所有边$(u,v)$,一定满足$(u,v)$的权值等于$F(u,v)$,并且从树中删除边$(u,v)$得到的两个连通块,包含$u$的连通块中的顶点集合恰好是$G$删除最小割后,与$u$保持连通的顶点集合,而包含$v$的连通块中的顶点集合恰好是$G$删除最小割后,与$v$保持连通的顶点集合。
很显然我们可以递归构建这样的一颗最小割树,任意选择当前顶点集合中两个不同顶点$u,v$,之后求出最小割$F(u,v)$,往$T$中加入一条边,之后将与$u$保持连通的顶点集合和与$v$保持连通的顶点集合分别递归处理。总的时间复杂度为$O(n^2+nU)$,其中$U$是每次求图$G$最大流的时间复杂度。
下面我们来证明一个重要的一些命题:
命题1:对于最小割树上的两条边$(a,b)$和$(b,c)$,一定满足$F(a,c)\leq \min(F(a,b),F(b,c))$。
证明:
这是很显然的,由于从图$G$移除$a$到$b$的最小割后,$c$落在了$b$连通块中,那么一定有$c$与$a$不连通,换句话说,就是$a$到$b$的最小割同时也是$c$与$a$的一个割,由此得到$F(a,c)\leq F(a,b)$,同理可以得到$F(a,c)\leq F(b,c)$。
命题2:对于最小割树上的两条边$(a,b)$和$(b,c)$,一定满足$F(a,c)\geq \min(F(a,b),F(b,c))$。
证明:
考虑从图$G$删除$a$与$c$的最小割后,不失一般性假设$b$与$c$连通。那么由于$c$与$b$不连通,因此可以断定$a$与$b$也不连通,即$a$与$c$的最小割同时也是一个$a$与$b$的割,因此可以推出$F(a,c)\geq F(a,b)$。当然如果$b$与$a$连通,那么我们则可以推出$F(a,c)\geq F(b,c)$。
命题4:对于最小割树上的两条边$(a,b)$和$(b,c)$,一定满足$F(a,c)= \min(F(a,b),F(b,c))$
证明:
结合命题1和命题2可以直接得出。
命题5:任意两点$u,v$的最小割$F(u,v)$一定等于最小割树上$u$到$v$的唯一路径中权重最小的边的权重(即最小瓶颈边)
证明:
可以根据树上路径的长度进行归纳法证明。
提供一道BZOJ题目。
不过说句实话,因为最小割的时间复杂为$O(n^2+nU)$,而你对所有顶点对直接跑最小割的时间复杂度也只是$O(n^2U)$而已,因此除非遇到非常多的最小割请求,否则最小割树并不是多好的选择。
Dinic解决单位图最大流
对于单位图,即除了源点和汇点外,其余顶点的要么只有一条入边且容量为$1$,要么只有一条出边且容量为$1$,其余边的容量任意,则Dinic可以在$O(V^{1/2}E)$时间复杂度内计算最大流。
如果能保证所有网络中边的容量都是$1$,那么时间复杂度可以约束到$O(\min(V^{2/3},E^{1/2})E)$。
提供一道需要用到这个性质的题目。
最小费用修复网络问题
问题1:给定一个包含$n$个顶点的网络图,顶点$n$是汇点。图中有$m$条单向边,第$i$条边当前的流量为$f_i$,容量为$c_i$。现在希望我们调整每条边的流量和容量,记调整后的流量为$f'_i$,容量为$c'_i$,满足下面条件:
- $\forall 1\leq i\leq n(0\leq f'_i\leq c'_i)$
- 每个顶点的入流和出流相等
增大减少第$i$条边的流量的单位费用为$a_i$,增大减少第$i$条边的容量的费用为$b_i$。要求计算最小费用,并且计算最小费用。
其中$c_i,f_i,c'_i,f'_i,a_i,b_i$都为非负整数。
我们考虑原始流为$f$,修正后的流为$f'$,记$\delta=f'-f$。那么可以发现$\delta$是个很特殊的流,我们需要最小化$\delta$的费用,也就是我们的结果。
首先我们加入一个超级源点$s$和超级汇点$t$。
要解决第一个条件,我们考虑第$i$条边$(u_i,v_i)$,我们可以在图中加入4条边。
- 从$u_i$到$v_i$连一条容量为$\max(c_i-f_i,0)$的费用为$a_i$的边。
- 从$v_i$到$u_i$连一条容量为$\min(f_i,c_i)$的费用为$a_i$的边。
- 从$u_i$到$v_i$连一条容量为无穷,费用为$a_i+b_i$的边。
- 从$v_i$到$u_i$连一条容量为$\max(f_i-c_i,0)$的费用为$a_i-b_i$的边。
这样我们就可以模拟修改流量和容量的操作了。
考虑某个入流为$x$,出流为$y$的顶点$u$,如果$x>y$,则其额外的流为$x-y$。我们需要想办法把它清除掉。做法就是我们从$s$到$u$连一条容量为$x-y$,费用为$0$的边,在最大流的前提下,这条边一定会被流满。同理如果$x\lt y$,其缺少的流为$y-x$,我们需要想办法填补它,做法就是从$u$到$t$连一条容量为$y-x$,费用为$0$的边,在最大流的前提下,这条边会被流满。
之后我们跑出最小费用最大流后,将所有与$s$和$t$相关的边删除后,得到的流就是我们求的$\delta$,费用为我们求的结果。
问题2:给定一个包含$n$个顶点的网络图,其中顶点$1$是源点,顶点$n$是汇点。图中有$m$条单向边,第$i$条边当前的流量为$f_i$,容量为$c_i$。现在希望我们调整每条边的流量和容量,记调整后的流量为$f'_i$,容量为$c'_i$,满足下面条件:
- $\forall 1\leq i\leq n(0\leq f'_i\leq c'_i)$
- 除了源点和汇点外,每个顶点的入流和出流相等
增大减少第$i$条边的流量的单位费用为$a_i$,增大减少第$i$条边的容量的费用为$b_i$。要求计算最小费用,并且计算最小费用。
其中$c_i,f_i,c'_i,f'_i,a_i,b_i$都为非负整数。
问题2和问题1的区别仅在于有两个特殊的点(源点和汇点)。如果我们直接在这样的图上跑最小费用最大流,那么由于最终每个顶点都会流量平衡(入流和出流相等),因此会导致所有流都被回退(即总流量为$0$)。解决这个问题的方法就是从顶点$n$到$1$加入一条流量为无穷费用为0的边,这样就能保证不需要回退所有流,就可以达到流量平衡(修正后的总流量会通过这条边发送到顶点$1$)。
提供一道题目。
费用流解决二分图标签问题
最近遇到了一些标签问题,所谓的标签问题是,给定两组非负变量$x_1,\ldots,x_n$以及$y_1,\ldots,y_m$,存在一些三元组$(i,j,c)$,要求$x_i+y_j\geq c$。要求找出一组可行解,存在多个可行解的情况下,要求$\sum_{i=1}^nx_i+\sum_{i=1}^my_i$最小化。
这个问题实际上可以使用Kuhn-Munkres算法$O(\max(n, m)^3)$计算得到。当然这个方案又两个问题,一个就是对于稀疏图效率较低,第二个问题是不能进一步扩展。即我们的约束条件修改为$x_i+y_j\leq c$,而总和$\sum_{i=1}^nx_i+\sum_{i=1}^my_i$的要求变成最大化。这个就没法用KM算法来求解了(不相信可以试一下XD)。
我们先将问题描述为线性规划形式:
\[\begin{aligned} \mathrm{min} &\sum_{i}x_i+\sum_{j}y_j\\ \mathrm{st.} &x_i+y_j\geq c_{i,j}\\ &x,y\geq 0 \end{aligned}\]再考虑它的对偶形式:
\[\begin{aligned} \mathrm{max} &\sum_{(i,j)\in E}c_{i,j}z_{i,j}\\ \mathrm{st.} &\sum_{(i,j)\in E}z_{i,j}\leq 1\\ &x,y\geq 0 \end{aligned}\]上面对偶形式实际上描述的是最大权二分图匹配,而利用Dijkstra优化的费用流在稀疏图上实际上可以跑到$O(VE\log_2V)$的时间复杂度。需要注意系数矩阵实际上是无向二分图的关联矩阵,是全幺模矩阵,因此线性规划的结果一定是整数。
再考虑扩展问题的线性规划形式:
\[\begin{aligned} \mathrm{max} &\sum_{i}x_i+\sum_{j}y_j\\ \mathrm{st.} &x_i+y_j\leq c_{i,j}\\ &x,y\geq 0 \end{aligned}\]其对偶形式为:
\[\begin{aligned} \mathrm{min} &\sum_{(i,j)\in E}c_{i,j}z_{i,j}\\ \mathrm{st.} &\sum_{(i,j)\in E}z_{i,j}\geq 1\\ &x,y\geq 0 \end{aligned}\]上面描述的实际上是最小权边覆盖问题,我们可以建模费用流来求解。需要注意的是系数矩阵实际上是无向二分图的关联矩阵,是全幺模矩阵,因此线性规划的结果一定是整数。我们可以用线性规划求解。
提供一些题目: