正则表达式
正则表达式语法
一般的正则表达式语法:
- $x$,$x$是一个简单字符,匹配一个同样的字符
- $xy$,其中$x$和$y$都是正则表达式,匹配一段文本$ab$,其中$x$与$a$匹配,$y$与$b$匹配。
- $x|y$,其中$x$和$y$都是正则表达式,匹配文本$a$,其中$x$与$a$匹配或$y$与$a$匹配。
- $x?$,$x+$,$x*$,分别表示匹配正则表达式$x$最多一次,至少一次,任意次。
我们可以通过圆括号来修改结合的优先级。
自动机
我们可以将正则表达式转换为自动机,比如a(bb)+a如下:

其中开始状态有一个单独的箭头指向,在图中为$s_0$。而匹配状态的一个双圆包含,图中为$s_4$。
上面图中展示的自动机为确定有穷自动机(deterministic finite automaton, DFA),因为每个顶点每个字符最多一条出边。当然的对应也有一种非确定有穷自动机(not deterministic finite automaton, NFA),如果某个顶点对于某类字符有多条出边,比如对于a(bb)+a,下图就是一个NFA。

我们可以添加一些不带标号的边,这样NFA看起来会更加简单易懂。

其中一条有向边上每个字符,表示即使没有输入新的字符,也可以从状态$s_3$转移到状态$s_1$。
正则表达式和NFA之间在功能上存在等价关系,每个NFA在功能上对应一个正则表达式,反之亦然。(同样,每个正则表达式在功能上都对应一个DFA,反之亦然)
从正则表达式构建NFA的方法首次由Thompson在他的1968年的CACM论文中提出。具体方法是通过将部分正则表达式转换为DFA的子图,之后合并这些子图得到完整的NFA。每个子图有开始顶点,但是没有匹配顶点,取而代之的是一个或多个悬置(dangling)边,这些边没有入点。
匹配单个字符的子图:
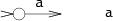
子图$e_1e_2$
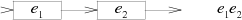
子图$e_1|e_2$。
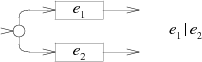
子图$e?$
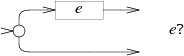
子图$e*$
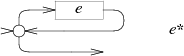
子图$e+$
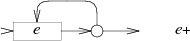
可以发现我们为每个正则表达式中的字符都创建正好一个顶点(除了括号),同时常数条出边。
我们可以通过之前讨论的方法移除所有没有标号的边,但是带有标号的NFA更加容易理解。
对于NFA,一般其匹配文本的算法是回溯,这在最坏情况下,时间复杂度是$O(2^m)$,$m$是文本的长度。大部分语言中(比如java)的正则表达式的实现方式都是回溯法,因为它支持更加复杂的语法。我们可以用形如$(a?)^na^n$的模式,以及使用$a^n$文本(其中指数表示的是前面内容重复$n$次),可以将时间复杂度劣化到$O(2^n)$。
考虑到DFA拥有线性的匹配性能,我们可以尝试将NFA转换为DFA来优化匹配性能,但是这对应的会花上更多的预处理时间和空间复杂度。下面我们讨论NFA转DFA的算法。设$V$为NFA中的顶点集合,$E$为其边集,其大小为$n$。我们对于任意$X\subseteq V$,都在DFA图中建立一个顶点$v_X$,对于任意字符$c$,记$Y$为$X$中顶点经过一条标号为$c$的边以及任意个没有标号的边所能达到的顶点集合,则我们在DFA中加入一条边$(v_X,v_Y)$,边的标号为$c$。
上面的算法可以构建一个DFA,但是预处理的空间复杂度和时间复杂度是$O(2^n)$。我们可以采用另外一种折中的方案,就是惰性计算DFA。可以发现大部分DFA状态都是不可能抵达的,因此我们可以在匹配的时候惰性计算新的DFA状态。这样可以有效减少时间消耗,且仅匹配所花费的时间实际上是非常少的。但是空间复杂度的问题还没解决,一个简单的方案就是使用一个带淘汰算法的数据结构来存储DFA(比如LRU、LFU算法),这样可以保证内存不会溢出。
下面讲一些将时间复杂度优化到$O(nm)$的方式。一种就是用回溯+记忆化,但是缺点就是使用递归,可能爆栈,并且空间时间复杂度为$O(nm)$。一种更加好的方式是在处理每个字符的时候标记之前整个序列可以抵达的状态集合,并从这些状态衍生出新的状态。如果希望某个字符串中提取最多的匹配正则表达式的不相交的子串,则可以在每次遇到匹配就结束,并在处理新字符的时候将开始状态加入到状态集合中。